We study the behavior of solutions of the semilinear problem
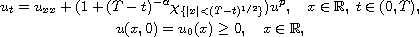
with
 and p>0 We describe, in terms of the parameters when the
solution is bounded and when it blows up. For blowing up solutions we find
the blow-up rate and the blow-up set.
and p>0 We describe, in terms of the parameters when the
solution is bounded and when it blows up. For blowing up solutions we find
the blow-up rate and the blow-up set.
Raul Ferreira
Abstract:
We study the behavior of solutions of the semilinear problem
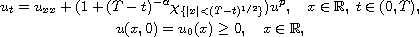
with
 and p>0 We describe, in terms of the parameters when the
solution is bounded and when it blows up. For blowing up solutions we find
the blow-up rate and the blow-up set.
and p>0 We describe, in terms of the parameters when the
solution is bounded and when it blows up. For blowing up solutions we find
the blow-up rate and the blow-up set.
Submitted July 13, 2017. Published January 22, 2018.
Math Subject Classifications: 35K58, 35B44, 35B40.
Key Words: Semilinear parabolic equation; blow-up; asymptotic behaviour.
Show me the PDF file (244 KB), TEX file for this article.
 |
Raul Ferreira Departamento de Matemática Aplicada Univ. Complutense de Madrid 28040 Madrid, Spain email: raul_ferreira@mat.ucm.es |
|---|
Return to the EJDE web page