Electron. J. Differential Equations,
Vol. 2018 (2018), No. 31, pp. 1-20.
Solutions for p(x)-Laplace equations with critical frequency
Xia Zhang, Chao Zhang, Huimin Gao
Abstract:
This article concerns the p(x)-Laplace equations with critical frequency
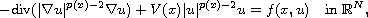
where
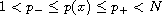 . We study this equation with the
potentials being zero. By using variational method, we obtain the existence
of nonnegative solutions. Moreover, if f(x,t) is odd in t, for any
. We study this equation with the
potentials being zero. By using variational method, we obtain the existence
of nonnegative solutions. Moreover, if f(x,t) is odd in t, for any
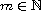 we derive m pairs of nontrivial solutions.
we derive m pairs of nontrivial solutions.
Submitted September 28, 2017. Published January 19, 2018.
Math Subject Classifications: 35J60.
Key Words: Variable exponent space; p(x)-Laplace; critical frequency;
weak solution.
Show me the PDF file (297 KB),
TEX file for this article.
 |
Xia Zhang
Department of Mathematics
Harbin Institute of Technology, China
email: zhangxia@hit.edu.cn
|
|---|
 |
Chao Zhang
Department of Mathematics
Harbin Institute of Technology, China
email: czhangmath@hit.edu.cn
|
|---|
| |
Huimin Gao
Department of Mathematics
Harbin Institute of Technology, China
email: 1576055240@qq.com
|
|---|
Return to the EJDE web page
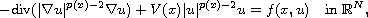
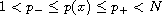 . We study this equation with the
potentials being zero. By using variational method, we obtain the existence
of nonnegative solutions. Moreover, if f(x,t) is odd in t, for any
. We study this equation with the
potentials being zero. By using variational method, we obtain the existence
of nonnegative solutions. Moreover, if f(x,t) is odd in t, for any
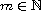 we derive m pairs of nontrivial solutions.
we derive m pairs of nontrivial solutions.

