We provide sufficient conditions for the existence of positive solutions of a nonlocal boundary value problem at resonance concerning a second order functional differential equation. The method is developed by inserting an exponential factor which depends on a suitable positive parameter
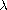 .
By this way a Green's kernel can be established and the problem is transformed
into an operator equation
.
By this way a Green's kernel can be established and the problem is transformed
into an operator equation
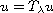 .
As it can be shown the well
known Krasnoselskii's fixed point theorem on cones in the Banach space C[0,1]
cannot be applied. More exactly, there is no (positive) value of the parameter
.
As it can be shown the well
known Krasnoselskii's fixed point theorem on cones in the Banach space C[0,1]
cannot be applied. More exactly, there is no (positive) value of the parameter
 for which the condensing property
for which the condensing property
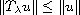 , with
, with
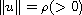 is satisfied. To overcome this fact we enlarge the space
is satisfied. To overcome this fact we enlarge the space
![$C[0,1]$](gifs/af.gif) and work in
and work in
![${\mathcal{L}^1[0,1]}$](gifs/ag.gif) where, now, Krasnoselskii's
fixed point theorem is applicable. Compactness criteria in this space are,
certainly, needed.
where, now, Krasnoselskii's
fixed point theorem is applicable. Compactness criteria in this space are,
certainly, needed.

