Electron. J. Differential Equations, Vol. 2018 (2018), No. 192, pp. 1-18.

Ground state solutions for asymptotically periodic Schrodinger-Poisson systems in R^2

Jing Chen, Sitong Chen, Xianhua Tang

Abstract:
This article concerns the planar Schrodinger-Poisson system
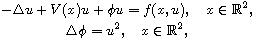
$$\displaylines{ -\Delta u+V(x)u+\phi u=f(x,u), \quad x\in \mathbb{R}^2,\cr \Delta \phi= u^2, \quad x\in \mathbb{R}^2, } $$
where V(x) and f(x, u) are periodic or asymptotically periodic in x. By combining the variational approach, the non-Nehari manifold approach and new analytic techniques, we establish the existence of ground state solutions for the above problem in the periodic and asymptotically periodic cases. In particular, in our study, f is not required to satisfy the Ambrosetti-Rabinowitz type condition or the Nehari-type monotonic condition.

Submitted March 5, 2018. Published November 27, 2018.
Math Subject Classifications: 35J20, 35J65.
Key Words: Planar Schrodinger-Poisson system; ground state solution; Logarithmic convolution potential.

Show me the PDF file (325 KB), TEX file for this article.

Jing Chen
School of Mathematics and Computing Sciences
Hunan University of Science and Technology
Xiangtan, Hunan 411201, China
email: cjhnust@aliyun.com
Sitong Chen
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: mathsitongchen@163.com
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn

Return to the EJDE web page