Electron. J. Differential Equations,
Vol. 2018 (2018), No. 189, pp. 1-12.
Exactness of the number of positive solutions to a singular
quasilinear problem
Giovanni Anello, Luca Vilasi
Abstract:
We study the exact multiplicity of positive solutions to the one-dimensional
Dirichlet problem
![$$\displaylines{
-(|u'|^{p-2}u')' = \lambda u^{s-1} - \mu u^{r-1} \quad \text{in } ]0,1[\cr
u(0) = u(1) = 0,
}$$](images/aa.png)
where
![$r\in]0,1[$](images/ab.png) ,
,
![$p\in]1,+\infty[$](images/ac.png) ,
,
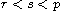 and
and
![$\lambda,\mu\in]0,+\infty[$](images/ae.png) .
We shed light, in particular, on the case
.
We shed light, in particular, on the case
![$r\in]0,\min\{s, p/(p+1)\}[$](images/af.png) ,
completely determining the bifurcation diagram and solving some related open
problems. Our approach relies upon quadrature methods.
,
completely determining the bifurcation diagram and solving some related open
problems. Our approach relies upon quadrature methods.
Submitted April 19, 2018. Published November 20, 2018.
Math Subject Classifications: 34B08, 34B16, 34B18.
Key Words: Exactness; singular problem; positive solution; quadrature method.
Show me the PDF file (146 KB),
TEX file for this article.
 |
Giovanni Anello
Department of Mathematics and Computer Sciences
Physical Sciences and Earth Sciences
University of Messina
Viale F. Stagno d'Alcontres 31
98166 Messina, Italy
email: ganello@unime.it
|
|---|
 |
Luca Vilasi
Department of Mathematics and Computer Sciences
Physical Sciences and Earth Sciences
University of Messina
Viale F. Stagno d'Alcontres 31
98166 Messina, Italy
email: lvilasi@unime.it
|
|---|
Return to the EJDE web page
![$$\displaylines{
-(|u'|^{p-2}u')' = \lambda u^{s-1} - \mu u^{r-1} \quad \text{in } ]0,1[\cr
u(0) = u(1) = 0,
}$$](images/aa.png)
![$r\in]0,1[$](images/ab.png) ,
,
![$p\in]1,+\infty[$](images/ac.png) ,
,
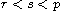 and
and
![$\lambda,\mu\in]0,+\infty[$](images/ae.png) .
We shed light, in particular, on the case
.
We shed light, in particular, on the case
![$r\in]0,\min\{s, p/(p+1)\}[$](images/af.png) ,
completely determining the bifurcation diagram and solving some related open
problems. Our approach relies upon quadrature methods.
,
completely determining the bifurcation diagram and solving some related open
problems. Our approach relies upon quadrature methods.

