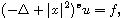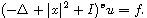Electron. J. Differential Equations,
Vol. 2018 (2018), No. 187, pp. 1-14.
Besov-Morrey spaces associated with Hermite operators and applications
to fractional Hermite equations
Nguyen Anh Dao, Nguyen Ngoc Trong, Le Xuan Truong
Abstract:
The purpose of this article is to establish the molecular decomposition
of the homogeneous Besov-Morrey spaces associated with the Hermite operator
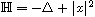 on the Euclidean space
on the Euclidean space
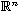 .
Particularly, we obtain some estimates for the operator
.
Particularly, we obtain some estimates for the operator
 on the Hermite-Besov-Morrey spaces and the regularity results to the
fractional Hermite equations
on the Hermite-Besov-Morrey spaces and the regularity results to the
fractional Hermite equations
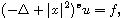
and
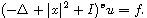
Our results generalize some results by Anh and Thinh [1].
Submitted September 26, 2018. Published November 20, 2018.
Math Subject Classifications: 42B35, 42B20.
Key Words: Fractional Hermite equations; Hermite-Besov-Morrey space;
molecular decomposition.
Show me the PDF file (283 KB),
TEX file for this article.
| |
Nguyen Anh Dao
Applied Analysis Research Group
Faculty of Mathematics and Statistics
Ton Duc Thang University
HoChiMinh City, Vietnam
email: daonguyenanh@tdtu.edu.vn
|
|---|
| |
Nguyen Ngoc Trong
Faculty of Mathematics and Computer Science
VUNHCM - University of Science
HoChiMinh city, Vietnam
email: trongnn37@gmail.com
|
|---|
 |
Le Xuan Truong
Department of Mathematics and Statistics
University of Economics
HoChiMinh City, Vietnam
email: lxuantruong@gmail.com
|
|---|
Return to the EJDE web page
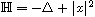 on the Euclidean space
on the Euclidean space
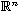 .
Particularly, we obtain some estimates for the operator
.
Particularly, we obtain some estimates for the operator
 on the Hermite-Besov-Morrey spaces and the regularity results to the
fractional Hermite equations
on the Hermite-Besov-Morrey spaces and the regularity results to the
fractional Hermite equations