Electron. J. Differential Equations,
Vol. 2018 (2018), No. 18, pp. 1-27.
Asymptotic stability and blow-up of solutions for an edge-degenerate wave
equation with singular potentials and several nonlinear source terms
of different sign
Feida Jiang, Yue Luan, Gang Li
Abstract:
We study the initial boundary value problem of an edge-degenerate wave equation.
The operator
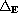 with edge degeneracy on the boundary
with edge degeneracy on the boundary
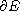 was investigated in the literature. We give the invariant sets
and the vacuum isolating behavior of solutions by introducing a family of
potential wells. We prove that the solution is global in time and exponentially
decays when the initial energy satisfies
was investigated in the literature. We give the invariant sets
and the vacuum isolating behavior of solutions by introducing a family of
potential wells. We prove that the solution is global in time and exponentially
decays when the initial energy satisfies
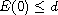 and
and
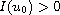 .
Moreover, we obtain the result of blow-up with initial energy
.
Moreover, we obtain the result of blow-up with initial energy
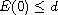 and
and
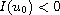 ,
and give a lower bound for the blow-up time
,
and give a lower bound for the blow-up time
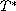 .
.
Submitted May 12, 2017. Published January 13, 2018.
Math Subject Classifications: 35L20, 35L80, 33B44.
Key Words: Edge-degenerate; potential function; blow-up; decay; global solution.
Show me the PDF file (341 KB),
TEX file for this article.
 |
Feida Jiang
College of Mathematics and Statistics
Nanjing University of Information Science and Technology
Nanjing 210044, China
email: jfd2001@163.com
|
|---|
 |
Yue Luan
College of Mathematics and Statistics
Nanjing University of Information Science and Technology
Nanjing 210044, China
email: yluan_sunflower@163.com
|
|---|
 |
Gang Li
College of Mathematics and Statistics
Nanjing University of Information Science and Technology
Nanjing 210044, China
email: ligang@nuist.edu.cn
|
|---|
Return to the EJDE web page
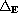 with edge degeneracy on the boundary
with edge degeneracy on the boundary
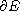 was investigated in the literature. We give the invariant sets
and the vacuum isolating behavior of solutions by introducing a family of
potential wells. We prove that the solution is global in time and exponentially
decays when the initial energy satisfies
was investigated in the literature. We give the invariant sets
and the vacuum isolating behavior of solutions by introducing a family of
potential wells. We prove that the solution is global in time and exponentially
decays when the initial energy satisfies
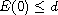 and
and
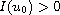 .
Moreover, we obtain the result of blow-up with initial energy
.
Moreover, we obtain the result of blow-up with initial energy
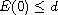 and
and
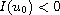 ,
and give a lower bound for the blow-up time
,
and give a lower bound for the blow-up time
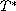 .
.


