Electron. J. Differential Equations,
Vol. 2018 (2018), No. 179, pp. 1-10.
Spectrum, global bifurcation and nodal solutions to Kirchhoff-type equations
Xiaofei Cao, Guowei Dai
Abstract:
In this article, we consider a Dancer-type unilateral global bifurcation
for the Kirchhoff-type problem
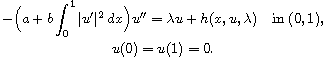
Under natural hypotheses on h, we show that
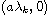 is a
bifurcation point of the above problem.
As applications we determine the interval of
is a
bifurcation point of the above problem.
As applications we determine the interval of
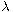 ,
in which there
exist nodal solutions for the Kirchhoff-type problem
,
in which there
exist nodal solutions for the Kirchhoff-type problem
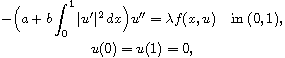
where f is asymptotically linear at zero and is asymptotically
3-linear at infinity. To do this, we also establish a complete
characterization of the spectrum of a nonlocal eigenvalue problem.
Submitted July 4, 2017. Published November 5, 2018.
Math Subject Classifications: 34C23, 47J10, 34C10.
Key Words: Bifurcation; spectrum; nonlocal problem; nodal solution.
Show me the PDF file (243 KB),
TEX file for this article.
 |
Xiaofei Cao
Faculty of Mathematics and Physics
Huaiyin Institute of Technology
Huaian 223003, China
email: caoxiaofei258@126.com
|
|---|
 |
Guowei Dai
School of Mathematical Sciences
Dalian University of Technology
Dalian 116024, China
email: daiguowei@dlut.edu.cn
|
|---|
Return to the EJDE web page
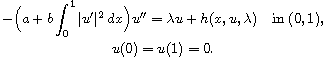
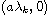 is a
bifurcation point of the above problem.
As applications we determine the interval of
is a
bifurcation point of the above problem.
As applications we determine the interval of
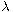 ,
in which there
exist nodal solutions for the Kirchhoff-type problem
,
in which there
exist nodal solutions for the Kirchhoff-type problem