Electron. J. Differential Equations,
Vol. 2018 (2018), No. 157, pp. 1-13.
Existence of ground state solutions for quasilinear Schrodinger equations
with variable potentials and almost necessary nonlinearities
Sitong Chen, Xianhua Tang
Abstract:
In this article we prove the existence of ground state solutions for the
quasilinear Schrodinger equation
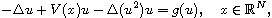
where
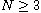 ,
,
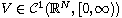 satisfies mild decay conditions and
satisfies mild decay conditions and
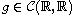 satisfies Berestycki-Lions conditions which are almost necessary.
In particular, we introduce some new inequalities and techniques
to overcome the lack of compactness.
satisfies Berestycki-Lions conditions which are almost necessary.
In particular, we introduce some new inequalities and techniques
to overcome the lack of compactness.
Submitted March 27, 2018. Published August 29, 2018.
Math Subject Classifications: 35J20, 35Q55.
Key Words: Quasilinear Schrodinger equation; ground state solution;
Berestycki-Lions conditions.
Show me the PDF file (284 KB),
TEX file for this article.
 |
Sitong Chen
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: mathsitongchen@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn
|
|---|
Return to the EJDE web page
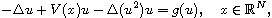
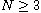 ,
,
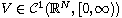 satisfies mild decay conditions and
satisfies mild decay conditions and
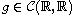 satisfies Berestycki-Lions conditions which are almost necessary.
In particular, we introduce some new inequalities and techniques
to overcome the lack of compactness.
satisfies Berestycki-Lions conditions which are almost necessary.
In particular, we introduce some new inequalities and techniques
to overcome the lack of compactness.

