Electron. J. Differential Equations,
Vol. 2018 (2018), No. 156, pp. 1-17.
Fractional p-Laplacian equations on Riemannian manifolds
Lifeng Guo, Binlin Zhang, Yadong Zhang
Abstract:
In this article we establish the theory of fractional Sobolev spaces
on Riemannian manifolds. As a consequence we investigate some important
properties, such as the reflexivity, separability, the embedding theorem
and so on. As an application, we consider fractional
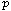 -Laplacian
equations with homogeneous Dirichlet boundary conditions
-Laplacian
equations with homogeneous Dirichlet boundary conditions

where
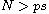 with
with
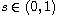 ,
,
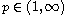 ,
,
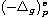 is
the fractional p-Laplacian on Riemannian manifolds, (M,g) is a compact
Riemannian
is
the fractional p-Laplacian on Riemannian manifolds, (M,g) is a compact
Riemannian
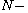 manifold,
manifold,
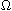 is an open bounded subset of M with
smooth boundary
is an open bounded subset of M with
smooth boundary
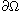 ,
and f is a Caratheodory function
satisfying the Ambrosetti-Rabinowitz type condition.
By using variational methods, we obtain the existence of nontrivial weak
solutions when the nonlinearity f satisfies sub-linear or super-linear
growth conditions.
,
and f is a Caratheodory function
satisfying the Ambrosetti-Rabinowitz type condition.
By using variational methods, we obtain the existence of nontrivial weak
solutions when the nonlinearity f satisfies sub-linear or super-linear
growth conditions.
Submitted August 18, 2017. Published August 22, 2018.
Math Subject Classifications: 35R01, 35R11, 35A15.
Key Words: Fractional p-Laplacian; Riemannian manifolds; variational methods.
Show me the PDF file (298 KB),
TEX file for this article.
 |
Lifeng Guo
School of Mathematics and Statistics
Northeast Petroleum University
Daqing 163318, China
email: lfguo1981@126.com
|
|---|
 |
Binlin Zhang
Department of Mathematics
Heilongjiang Institute of Technology
Harbin 150050, China
email: zhangbinlin2012@outlook.com
|
|---|
 |
Yadong Zhang
School of Mathematics and Statistics
Northeast Petroleum University
Daqing 163318, China
email: chichidong@foxmail.com
|
|---|
Return to the EJDE web page



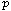 -Laplacian
equations with homogeneous Dirichlet boundary conditions
-Laplacian
equations with homogeneous Dirichlet boundary conditions

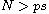 with
with
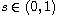 ,
,
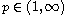 ,
,
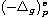 is
the fractional p-Laplacian on Riemannian manifolds, (M,g) is a compact
Riemannian
is
the fractional p-Laplacian on Riemannian manifolds, (M,g) is a compact
Riemannian
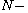 manifold,
manifold,
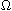 is an open bounded subset of M with
smooth boundary
is an open bounded subset of M with
smooth boundary
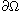 ,
and f is a Caratheodory function
satisfying the Ambrosetti-Rabinowitz type condition.
By using variational methods, we obtain the existence of nontrivial weak
solutions when the nonlinearity f satisfies sub-linear or super-linear
growth conditions.
,
and f is a Caratheodory function
satisfying the Ambrosetti-Rabinowitz type condition.
By using variational methods, we obtain the existence of nontrivial weak
solutions when the nonlinearity f satisfies sub-linear or super-linear
growth conditions.