Electron. J. Differential Equations,
Vol. 2018 (2018), No. 151, pp. 1-26.
Stability of ground states for a nonlinear parabolic equation
Luca Bisconti, Matteo Franca
Abstract:
We consider the Cauchy-problem for the parabolic equation
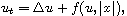
where
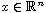 ,
,
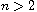 , and
, and
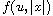 is either critical or
supercritical with respect to the Joseph-Lundgren exponent.
In particular, we improve and generalize some known results concerning
stability and weak asymptotic stability of positive ground states.
is either critical or
supercritical with respect to the Joseph-Lundgren exponent.
In particular, we improve and generalize some known results concerning
stability and weak asymptotic stability of positive ground states.
Submitted April 5, 2018. Published August 10, 2018.
Math Subject Classifications: 35k58, 35k91, 34e05, 35b08, 35b35.
Key Words: Weak asymptotic stability; supercritical parabolic equations;
ground states; asymptotic expansion.
Show me the PDF file (447 KB),
TEX file for this article.
 |
Luca Bisconti
Dipartimento di Matematica e Informatica "U. Dini"
Università degli Studi di Firenze
Via S. Marta 3, I-50139 Firenze, Italy
email: luca.bisconti@unifi.it
|
|---|
 |
Matteo Franca
Dipartimento di Ingegneria Industriale e Scienze Matematiche
Università Politecnica delle Marche
Via Brecce Bianche, I-60131 Ancona, Italy
email: franca@dipmat.univpm.it
|
|---|
Return to the EJDE web page
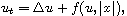
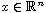 ,
,
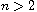 , and
, and
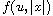 is either critical or
supercritical with respect to the Joseph-Lundgren exponent.
In particular, we improve and generalize some known results concerning
stability and weak asymptotic stability of positive ground states.
is either critical or
supercritical with respect to the Joseph-Lundgren exponent.
In particular, we improve and generalize some known results concerning
stability and weak asymptotic stability of positive ground states.

