Electron. J. Differential Equations,
Vol. 2018 (2018), No. 145, pp. 1-13.
The Poisson equation from non-local to local
Umberto Biccari, Victor Hernandez-Santamaria
Abstract:
We analyze the limiting behavior as
 of the solution to the
fractional Poisson equation
of the solution to the
fractional Poisson equation
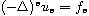 ,
,
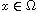 with
homogeneous Dirichlet boundary conditions
with
homogeneous Dirichlet boundary conditions
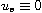 ,
,
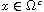 .
We show that
.
We show that
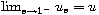 , with
, with
 ,
,
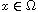 and
and
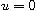 ,
,
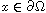 .
Our results are complemented by a discussion
on the rate of convergence and on extensions to the parabolic setting.
.
Our results are complemented by a discussion
on the rate of convergence and on extensions to the parabolic setting.
Submitted January 22, 2018. Published July 17, 2018.
Math Subject Classifications: 35B30, 35R11, 35S05.
Key Words: Fractional Laplacian; elliptic equations; weak solutions.
Show me the PDF file (670 KB),
TEX file for this article.
 |
Umberto Biccari
DeustoTech, University of Deusto
48007 Bilbao, Basque Country, Spain
email: umberto.biccari@deusto.es, u.biccari@gmail.com
|
|---|
 |
Víctor Hernández-Santamaría
DeustoTech, University of Deusto
48007 Bilbao, Basque Country, Spain
email: victor.santamaria@deusto.es
|
|---|
Return to the EJDE web page
 of the solution to the
fractional Poisson equation
of the solution to the
fractional Poisson equation
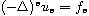 ,
,
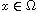 with
homogeneous Dirichlet boundary conditions
with
homogeneous Dirichlet boundary conditions
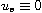 ,
,
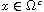 .
We show that
.
We show that
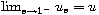 , with
, with
 ,
,
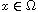 and
and
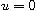 ,
,
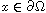 .
Our results are complemented by a discussion
on the rate of convergence and on extensions to the parabolic setting.
.
Our results are complemented by a discussion
on the rate of convergence and on extensions to the parabolic setting.

