Electron. J. Differential Equations,
Vol. 2018 (2018), No. 139, pp. 1-13.
Maximal estimates for fractional Schrodinger equations with spatial
variable coefficient
Bo-Wen Zheng
Abstract:
Let
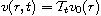 be the solution to a fractional
Schrodinger equation where the coefficient of Laplacian depends
on the spatial variable. We prove some weighted
be the solution to a fractional
Schrodinger equation where the coefficient of Laplacian depends
on the spatial variable. We prove some weighted
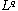 estimates for
the maximal operator generated by
estimates for
the maximal operator generated by
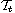 with initial data
in a Sobolev-type space.
with initial data
in a Sobolev-type space.
Submitted May 28, 2017. Published July 3, 2018.
Math Subject Classifications: 35B65, 35Q40, 35Q55.
Key Words: Schrodinger equation with spatial variable coefficient;
maximal estimate; Hankel-Sobolev space.
Show me the PDF file (289 KB),
TEX file for this article.
 |
Bo-wen Zheng
College of Sciences
China Jiliang University
Hangzhou 310018, China
email: bwen_zj1516@126.com, 17a0802126@cjlu.edu.cn
|
|---|
Return to the EJDE web page
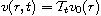 be the solution to a fractional
Schrodinger equation where the coefficient of Laplacian depends
on the spatial variable. We prove some weighted
be the solution to a fractional
Schrodinger equation where the coefficient of Laplacian depends
on the spatial variable. We prove some weighted
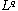 estimates for
the maximal operator generated by
estimates for
the maximal operator generated by
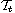 with initial data
in a Sobolev-type space.
with initial data
in a Sobolev-type space.
