Electron. J. Differential Equations,
Vol. 2018 (2018), No. 120, pp. 1-9.
Jacobi-Maupertuis metric of Lienard type equations and Jacobi last multiplier
Sumanto Chanda, Anindya Ghose-Choudhury, Partha Guha
Abstract:
We present a construction of the Jacobi-Maupertuis (JM) principle for an
equation of the Lienard type,
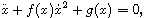
using Jacobi's last multiplier. The JM metric allows us to reformulate the
Newtonian equation of motion for a variable mass as a geodesic equation
for a Riemannian metric. We illustrate the procedure with examples of
Painleve-Gambier XXI, the Jacobi equation and the Henon-Heiles system.
Submitted January 15, 2018. Published June 15, 2018.
Math Subject Classifications: 34C14, 34C20.
Key Words: Jacobi-Maupertuis metric; position-dependent mass;
Jacobi's last multiplier.
Show me the PDF file (220 KB),
TEX file for this article.
Sumanto Chanda
S. N. Bose National Centre for Basic Sciences
JD Block, Sector-3
Salt Lake, Kolkata 700098, India
email: sumanto12@bose.res.in
|
Anindya Ghose-Choudhury
Department of Physics, Surendranath College
24/2 Mahatma Gandhi Road
Kolkata 700009, India
email: aghosechoudhury@gmail.com
|
Partha Guha
Instituto de Fíisica de São Carlos; IFSC/USP
Universidade de São Paulo Caixa Postal 369
CEP 13560-970, São Carlos, SP, Brazil
email: partha@bose.res.in
|
Return to the EJDE web page