Electron. J. Differential Equations,
Vol. 2018 (2018), No. 12, pp. 1-23.
Existence of solutions for a fractional elliptic problem with
critical Sobolev-Hardy nonlinearities in R^N
Lingyu Jin, Shaomei Fang
Abstract:
In this article, we study the fractional elliptic equation with critical
Sobolev-Hardy nonlinearity

where
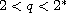 ,
,
 ,
,
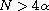 ,
,
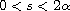 ,
,
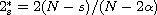 is the critical Sobolev-Hardy exponent,
is the critical Sobolev-Hardy exponent,
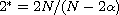 is the critical Sobolev exponent,
is the critical Sobolev exponent,
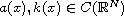 .
Through a compactness
analysis of the functional associated, we
obtain the existence of positive solutions under
certain assumptions on
.
Through a compactness
analysis of the functional associated, we
obtain the existence of positive solutions under
certain assumptions on
 .
.
Submitted April 8, 2017. Published January 10, 2018.
Math Subject Classifications: 35J10, 35J20, 35J60.
Key Words: Fractional Laplacian; compactness; positive solution;
unbounded domain; Sobolev-Hardy nonlinearity.
Show me the PDF file (344 KB),
TEX file for this article.
 |
Lingyu Jin
Department of Mathematics
South China Agricultural University
Guangzhou 510642, China
email: jinlingyu300@126.com
|
|---|
 |
Shaomei Fang
Department of Mathematics
South China Agricultural University
Guangzhou 510642, China
email: fangshaomeidz90@126.com
|
|---|
Return to the EJDE web page

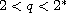 ,
,
 ,
,
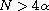 ,
,
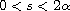 ,
,
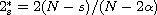 is the critical Sobolev-Hardy exponent,
is the critical Sobolev-Hardy exponent,
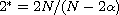 is the critical Sobolev exponent,
is the critical Sobolev exponent,
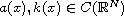 .
Through a compactness
analysis of the functional associated, we
obtain the existence of positive solutions under
certain assumptions on
.
Through a compactness
analysis of the functional associated, we
obtain the existence of positive solutions under
certain assumptions on
 .
.

