Electron. J. Differential Equations,
Vol. 2018 (2018), No. 110, pp. 1-24.
Global regularity in Orlicz-Morrey spaces of solutions to nondivergence
elliptic equations with VMO coefficients
Vagif S. Guliyev, Aysel A. Ahmadli, Mehriban N. Omarova, Lubomira Softova
Abstract:
We show continuity in generalized Orlicz-Morrey spaces
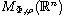 of sublinear integral operators generated by Calderon-Zygmund operator
and their commutators with BMO functions. The obtained estimates are used to
study global regularity of the solution of the Dirichlet problem for linear
uniformly elliptic operator
of sublinear integral operators generated by Calderon-Zygmund operator
and their commutators with BMO functions. The obtained estimates are used to
study global regularity of the solution of the Dirichlet problem for linear
uniformly elliptic operator
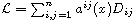 with discontinuous coefficients. We show that
with discontinuous coefficients. We show that
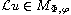 implies the second-order
derivatives belong to
implies the second-order
derivatives belong to
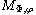 .
.
Submitted September 11, 2017. Published May 10, 2018
Math Subject Classifications: 35J25, 35B40, 42B20, 42B35, 46E30.
Key Words: Generalized Orlicz-Morrey spaces; Calderon-Zygmund integrals;
commutators; VMO; elliptic equations; Dirichlet problem.
Show me the PDF file (375 KB),
TEX file for this article.
 |
Vagif S. Guliyev
Ahi Evran University
Department of Mathematics
40100 Kirsehir, Turkey
email: vagif@guliyev.com
|
|---|
 |
Aysel A. Ahmadli
Dumlupinar University
Department of Mathematics
40100 Kytahya, Turkey
email: aysel.ahmadli@gmail.com
|
|---|
 |
Mehriban N. Omarova
Baku State University
AZ1141 Baku, Azerbaijan
email: mehribanomarova@yahoo.com
|
|---|
 |
Lubomira G. Softova
Department of Mathematics
University of Salerno
Fisciano, Italy
email: lsoftova@unisa.it
|
|---|
Return to the EJDE web page
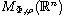 of sublinear integral operators generated by Calderon-Zygmund operator
and their commutators with BMO functions. The obtained estimates are used to
study global regularity of the solution of the Dirichlet problem for linear
uniformly elliptic operator
of sublinear integral operators generated by Calderon-Zygmund operator
and their commutators with BMO functions. The obtained estimates are used to
study global regularity of the solution of the Dirichlet problem for linear
uniformly elliptic operator
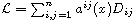 with discontinuous coefficients. We show that
with discontinuous coefficients. We show that
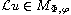 implies the second-order
derivatives belong to
implies the second-order
derivatives belong to
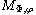 .
.



