Electron. J. Differential Equations,
Vol. 2018 (2018), No. 105, pp. 1-24.
Existence of solutions to nonlinear p-Laplacian fractional
differential equations with higher-order derivative terms
You-Hui Su, Yongzhen Yun, Dongdong Wang, Weimin Hu
Abstract:
In this article, we discuss the existence of positive solution to a
nonlinear p-Laplacian fractional differential equation
whose nonlinearity contains a higher-order derivative
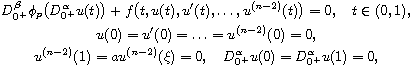
where
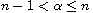 ,
,
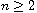 ,
,
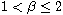 ,
,
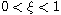 ,
,
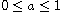 and
and
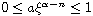 ,
,
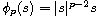 ,
,
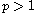 ,
,
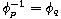 ,
,
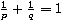 .
.
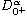 ,
,
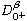 are the standard Riemann-Liouville fractional derivatives, and
are the standard Riemann-Liouville fractional derivatives, and
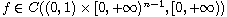 .
The Green's function of the fractional differential equation mentioned above
and its relevant properties are presented, and some novel results on the
existence of positive solution are established by using the mixed monotone
fixed point theorem and the upper and lower solution method. The interesting
of this paper is that the nonlinearity involves the higher-order derivative,
and also, two examples are given in this paper to illustrate our main results
from the perspective of application.
.
The Green's function of the fractional differential equation mentioned above
and its relevant properties are presented, and some novel results on the
existence of positive solution are established by using the mixed monotone
fixed point theorem and the upper and lower solution method. The interesting
of this paper is that the nonlinearity involves the higher-order derivative,
and also, two examples are given in this paper to illustrate our main results
from the perspective of application.
Submitted June 19, 2016. Published May 7, 2018.
Math Subject Classifications: 34B25, 34B18, 35G30.
Key Words: Fractional differential equation; Green's function;
p-Laplacian operator; upper and lower solution method.
Show me the PDF file (315 KB),
TEX file for this article.
 |
You-Hui Su
School of Mathematics and Physics
Xuzhou University of Technology
Xuzhou, Jiangsu 221018, China
email: suyh02@163.com, suyouhui@xzit.edu.cn
|
|---|
 |
Yongzhen Yun
College of Science
Hohai University
Nanjing, Jiangsu 211100, China
email: yongzhen0614@163.com
|
|---|
 |
Dongdong Wang
School of Mathematics and Physics
Xuzhou University of Technology
Xuzhou, Jiangsu 221018, China
email: wdd@xzit.edu.cn
|
|---|
 |
Weimin Hu
School of Mathematics and Statistic
Yili Normal University
Yining, Xinjiang 835000, China
email: hwm680702@163.com
|
|---|
Return to the EJDE web page
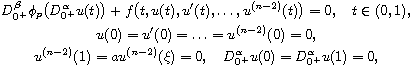
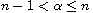 ,
,
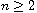 ,
,
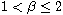 ,
,
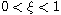 ,
,
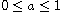 and
and
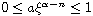 ,
,
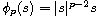 ,
,
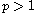 ,
,
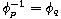 ,
,
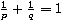 .
.
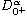 ,
,
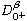 are the standard Riemann-Liouville fractional derivatives, and
are the standard Riemann-Liouville fractional derivatives, and
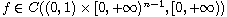 .
The Green's function of the fractional differential equation mentioned above
and its relevant properties are presented, and some novel results on the
existence of positive solution are established by using the mixed monotone
fixed point theorem and the upper and lower solution method. The interesting
of this paper is that the nonlinearity involves the higher-order derivative,
and also, two examples are given in this paper to illustrate our main results
from the perspective of application.
.
The Green's function of the fractional differential equation mentioned above
and its relevant properties are presented, and some novel results on the
existence of positive solution are established by using the mixed monotone
fixed point theorem and the upper and lower solution method. The interesting
of this paper is that the nonlinearity involves the higher-order derivative,
and also, two examples are given in this paper to illustrate our main results
from the perspective of application.



