In the domain
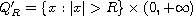 we consider the problem
we consider the problem
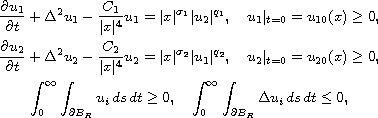
where
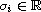 ,
,
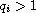 ,
,
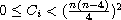 ,
,
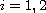 .
Sufficient condition for the nonexistence of global solutions
is obtained.The proof is based on the method of test functions.
.
Sufficient condition for the nonexistence of global solutions
is obtained.The proof is based on the method of test functions.
Shirmayil Bagirov
Abstract:
In the domain
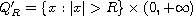 we consider the problem
we consider the problem
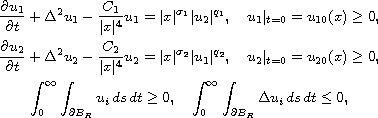
where
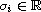 ,
,
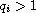 ,
,
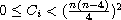 ,
,
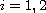 .
Sufficient condition for the nonexistence of global solutions
is obtained.The proof is based on the method of test functions.
.
Sufficient condition for the nonexistence of global solutions
is obtained.The proof is based on the method of test functions.
Submitted November 12, 2017. Published January 6, 2018.
Math Subject Classifications: 35A01, 35B33, 35K52, 35K91.
Key Words: System of semilinear parabolic equation; biharmonic operator;
global solution; critical exponent; method of test functions.
Show me the PDF file (254 KB), TEX file for this article.
 |
Shirmayil Bagirov Institute of Mathematics and Mechanics of NAS of Azerbaijan Baku, Azerbaijan email: sh_bagirov@yahoo.com |
|---|
Return to the EJDE web page