Electron. J. Differential Equations,
Vol. 2018 (2018), No. 04, pp. 1-20.
Existence and asymptotic behavior of solutions of the
Dirichlet problem for a nonlinear pseudoparabolic equation
Le Thi Phuong Ngoc, Dao Thi Hai Yen, Nguyen Thanh Long
Abstract:
This article concerns the initial-boundary value problem for nonlinear
pseudo-parabolic equation
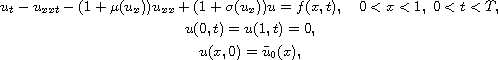
where f,
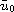 ,
,
 ,
,
 are given functions. Using the
Faedo-Galerkin method and the compactness method, we prove that there exists
a unique weak solution u such that
are given functions. Using the
Faedo-Galerkin method and the compactness method, we prove that there exists
a unique weak solution u such that
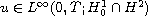 ,
,
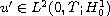 and
and
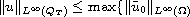 ,
,
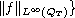 .
Also we prove that the problem has a unique
global solution with
.
Also we prove that the problem has a unique
global solution with
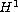 -norm
decaying exponentially as
-norm
decaying exponentially as
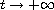 .
Finally, we establish the existence and uniqueness of a weak solution of
the problem associated with a periodic condition.
.
Finally, we establish the existence and uniqueness of a weak solution of
the problem associated with a periodic condition.
Submitted January 27, 2017. Published January 4, 2018.
Math Subject Classifications: 34B60, 35K55, 35Q72, 80A30.
Key Words: Nonlinear pseudoparabolic equation; asymptotic behavior;
exponential decay; periodic weak solution;
Faedo-Galerkin method.
Show me the PDF file (305 KB),
TEX file for this article.
 |
Le Thi Phuong Ngoc
University of Khanh Hoa
01 Nguyen Chanh Str., Nha Trang City, Vietnam
email: ngoc1966@gmail.com
|
|---|
 |
Dao Thi Hai Yen
Department of Natural Science
Phu Yen University
18 Tran Phu Str., Ward 7, Tuy Hoa City, Vietnam
email: haiyennbh@yahoo.com
|
|---|
 |
Nguyen Thanh Long
Department of Mathematics and Computer Science
VNUHCM - University of Science
227 Nguyen Van Cu Str., Dist. 5, HoChiMinh City, Vietnam
email: longnt2@gmail.com
|
|---|
Return to the EJDE web page
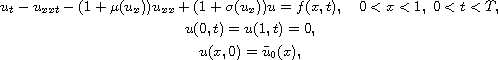
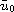 ,
,
 ,
,
 are given functions. Using the
Faedo-Galerkin method and the compactness method, we prove that there exists
a unique weak solution u such that
are given functions. Using the
Faedo-Galerkin method and the compactness method, we prove that there exists
a unique weak solution u such that
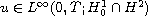 ,
,
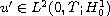 and
and
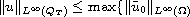 ,
,
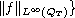 .
Also we prove that the problem has a unique
global solution with
.
Also we prove that the problem has a unique
global solution with
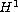 -norm
decaying exponentially as
-norm
decaying exponentially as
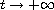 .
Finally, we establish the existence and uniqueness of a weak solution of
the problem associated with a periodic condition.
.
Finally, we establish the existence and uniqueness of a weak solution of
the problem associated with a periodic condition.


