In this article, we establish the global bifurcation result from the trivial solutions axis or from infinity for the Monge-Ampere equations with non-differentiable nonlinearity. By applying the above result, we shall determine the interval of
 ,
in which there exist
radial solutions for the following Monge-Amp\`ere equation
,
in which there exist
radial solutions for the following Monge-Amp\`ere equation
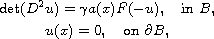
where
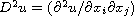 is the Hessian
matrix of u, where B is the unit open ball of
is the Hessian
matrix of u, where B is the unit open ball of
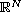 ,
,
 is a positive parameter.
is a positive parameter.
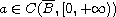 is a radially symmetric weighted function and
is a radially symmetric weighted function and
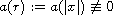 on any subinterval of [0, 1] and the nonlinear term
on any subinterval of [0, 1] and the nonlinear term
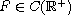 but is not necessarily differentiable
at the origin and infinity.
We use global interval bifurcation techniques to prove our main results.
but is not necessarily differentiable
at the origin and infinity.
We use global interval bifurcation techniques to prove our main results.
