Electron. J. Differential Equations,
Vol. 2017 (2017), No. 97, pp. 1-13.
Infinitely many solutions for fractional Schrodinger-Poisson
systems with sign-changing potential
Jianhua Chen, Xianhua Tang, Huxiao Luo
Abstract:
In this article, we prove the existence of multiple solutions for
following fractional Schrodinger-Poisson system with sign-changing
potential
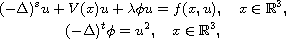
where
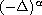 denotes the fractional Laplacian of order
denotes the fractional Laplacian of order
 ,
and the potential V is allowed to be sign-changing.
Under certain assumptions on f, we obtain infinitely many solutions
for this system.
,
and the potential V is allowed to be sign-changing.
Under certain assumptions on f, we obtain infinitely many solutions
for this system.
Submitted June 28, 2016. Published April 5, 2017.
Math Subject Classifications: 35J60, 35J20.
Key Words: Fractional Schrodinger-Poisson systems; sign-changing potential;
symmetric mountain pass theorem; infinitely many solutions.
Show me the PDF file (263 KB),
TEX file for this article.
 |
Jianhua Chen
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: cjh19881129@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: tangxh@mail.csu.edu.cn
|
|---|
 |
Huxiao Luo
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: wshrm7@126.com
|
|---|
Return to the EJDE web page
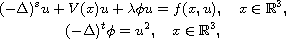
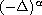 denotes the fractional Laplacian of order
denotes the fractional Laplacian of order
 ,
and the potential V is allowed to be sign-changing.
Under certain assumptions on f, we obtain infinitely many solutions
for this system.
,
and the potential V is allowed to be sign-changing.
Under certain assumptions on f, we obtain infinitely many solutions
for this system.


