Electron. J. Differential Equations, Vol. 2017 (2017), No. 93, pp. 1-15.

Multiplicity of solutions for nonperiodic perturbed fractional Hamiltonian systems

Abderrazek Benhassine

Abstract:
In this article, we prove the existence and multiplicity of nontrivial solutions for the nonperiodic perturbed fractional Hamiltonian systems
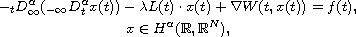
$$\displaylines{ -_{t}D^{\alpha}_{\infty}(_{-\infty}D^{\alpha}_{t}x(t)) -\lambda L(t)\cdot x(t)+\nabla W(t,x(t))=f(t),\cr x\in H^{\alpha}(\mathbb{R}, \mathbb{R}^{N}), }$$
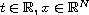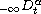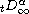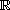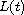where $\alpha \in (1/2 , 1],\; \lambda> 0 $ is a parameter, $t\in \mathbb{R}, x\in \mathbb{R}^N$, ${}_{-\infty}D^{\alpha}_{t}$ and ${}_{t}D^{\alpha}_{\infty}$ are left and right Liouville-Weyl fractional derivatives of order $\alpha$ on the whole axis $\mathbb{R}$ respectively, the matrix $L(t)$ is not necessary positive definite for all 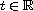$t\in \mathbb{R}$ nor coercive, 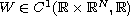$W \in C^{1}(\mathbb{R}\times\mathbb{R}^{N},\mathbb{R})$ and $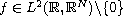f\in L^{2}(\mathbb{R},\mathbb{R}^{N})\backslash\{0\}$ small enough. Replacing the Ambrosetti-Rabinowitz Condition by general superquadratic assumpt ions, we establish the existence and multiplicity results for the above system. Some examples are also given to illustrate our results.

Submitted December 13, 2016. Published March 30, 2017.
Math Subject Classifications: 34C37, 35A15, 37J45.
Key Words: Fractional Hamiltonian systems; critical point; variational methods.

Show me the PDF file (271 KB), TEX file for this article.

Abderrazek Benhassine
Dept. of Mathematics
High Institut of Informatics and Mathematics
5000, Monastir, Tunisia
email: ab.hassine@yahoo.com

Return to the EJDE web page