Electron. J. Differential Equations,
Vol. 2017 (2017), No. 91, pp. 1-17.
Existence and multiplicity of solutions for nonlinear
Dirac-Poisson systems
Jian Zhang, Wen Zhang, Xianhua Tang
Abstract:
This article concerns the nonlinear Dirac-Poisson system
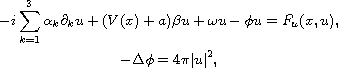
in
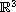 ,
where V(x) is a potential function and F(x,u)
is an asymptotically quadratic nonlinearity modeling various types
of interaction. Since the effects of the nonlocal term, we use some
special techniques to deal with the nonlocal term. Moreover,
the existence of infinitely many stationary solutions is obtained
for system with periodicity assumption via variational methods.
,
where V(x) is a potential function and F(x,u)
is an asymptotically quadratic nonlinearity modeling various types
of interaction. Since the effects of the nonlocal term, we use some
special techniques to deal with the nonlocal term. Moreover,
the existence of infinitely many stationary solutions is obtained
for system with periodicity assumption via variational methods.
Submitted December 17, 2016. Published March 29, 2017.
Math Subject Classifications: 49J35, 35Q40, 81V10.
Key Words: Dirac-Poisson system; asymptotically quadratic; variational methods;
strongly indefinite functionals.
Show me the PDF file (308 KB),
TEX file for this article.
 |
Jian Zhang
School of Mathematics and Statistics
Hunan University of Commerce
Changsha, 410205 Hunan, China
email: zhangjian433130@163.com
|
|---|
 |
Wen Zhang
School of Mathematics and Statistics
Hunan University of Commerce
Changsha, 410205 Hunan, China
email: zwmath2011@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn
|
|---|
Return to the EJDE web page
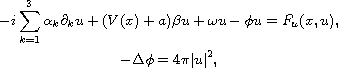
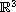 ,
where V(x) is a potential function and F(x,u)
is an asymptotically quadratic nonlinearity modeling various types
of interaction. Since the effects of the nonlocal term, we use some
special techniques to deal with the nonlocal term. Moreover,
the existence of infinitely many stationary solutions is obtained
for system with periodicity assumption via variational methods.
,
where V(x) is a potential function and F(x,u)
is an asymptotically quadratic nonlinearity modeling various types
of interaction. Since the effects of the nonlocal term, we use some
special techniques to deal with the nonlocal term. Moreover,
the existence of infinitely many stationary solutions is obtained
for system with periodicity assumption via variational methods.


