Electron. J. Differential Equations,
Vol. 2017 (2017), No. 73, pp. 1-26.
Decay rates for solutions to thermoelastic Bresse systems of types I and III
Fernando A. Gallego, Jaime E. Munoz Rivera
Abstract:
In this article, we study the energy decay for the thermoelastic Bresse system
in the whole line with two dissipative mechanisms, given by heat conduction
(Types I and III). We prove that the decay rate of the solutions are very slow.
More precisely, we show that the solutions decay with the rate of
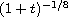 in the
in the
 -norm,
whenever the initial data belongs to
-norm,
whenever the initial data belongs to
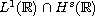 for a suitable s.
The wave speeds of propagation have influence on the decay rate with respect
to the regularity of the initial data. This phenomenon is known as
regularity-loss. The main tool used to prove our results is the
energy method in the Fourier space.
for a suitable s.
The wave speeds of propagation have influence on the decay rate with respect
to the regularity of the initial data. This phenomenon is known as
regularity-loss. The main tool used to prove our results is the
energy method in the Fourier space.
Submitted February 17, 2016. Published March 15, 2017.
Math Subject Classifications: 35B35, 35L55, 93D20.
Key Words: Decay rate; heat conduction; Bresse system; thermoelasticity.
Show me the PDF file (339 KB),
TEX file for this article.
 |
Fernando A. Gallego
Centre de Robotique (CAOR), MINES Paristech
PSL Research University, 60 boulevard Saint-Michel
75272 Paris Cedex 06, France
email: ferangares@gmail.com
|
|---|
 |
Jaime E. Muñoz Rivera
Laboratório de Computução Científica, LNCC
Petrópolis, 25651-070, RJ, Brazil
email: rivera@lncc.br, rivera@im.ufrj.br
|
|---|
Return to the EJDE web page
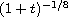 in the
in the
 -norm,
whenever the initial data belongs to
-norm,
whenever the initial data belongs to
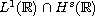 for a suitable s.
The wave speeds of propagation have influence on the decay rate with respect
to the regularity of the initial data. This phenomenon is known as
regularity-loss. The main tool used to prove our results is the
energy method in the Fourier space.
for a suitable s.
The wave speeds of propagation have influence on the decay rate with respect
to the regularity of the initial data. This phenomenon is known as
regularity-loss. The main tool used to prove our results is the
energy method in the Fourier space.

