Electron. J. Differential Equations, Vol. 2017 (2017), No. 58, pp. 1-25.

Existence of global solutions and decay estimates for a viscoelastic Petrovsky equation with a delay term in the non-linear internal feedback

Nadia Mezouar, Mama Abdelli, Amira Rachah

Abstract:
In this article we consider a nonlinear viscoelastic Petrovsky equation in a bounded domain with a delay term in the weakly nonlinear internal feedback:
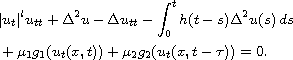
$$\eqalign{ &|u_t|^{l}u_{tt} +\Delta^2 u -\Delta u_{tt} -\int_0^t h(t-s)\Delta^2 u(s)\,ds\cr &+\mu_1g_1(u_t(x,t)) +\mu_2g_2(u_t(x,t-\tau))=0. }$$
We prove the existence of global solutions in suitable Sobolev spaces by using the energy method combined with Faedo-Galarkin method under condition on the weight of the delay term in the feedback and the weight of the term without delay. Furthermore, we study general stability estimates by using some properties of convex functions.

Submitted February 1, 2017. Published February 27, 2017.
Math Subject Classifications: 35A01, 74G25, 35B35, 35B25, 26A51.
Key Words: Global solution; delay term; general decay; multiplier method; weak frictional damping; convexity; viscoelastic Petrovsky equation.

Show me the PDF file (331 KB), TEX file for this article.

Nadia Mezouar
Laboratoire of Mathematics
Djillali Liabes University
P.O. Box 89, Sidi Bel Abbes 22000, Algeria
email: nadia_dz12@yahoo.fr
  Mama Abdelli
Laboratoire of Mathematics
Djillali Liabes University
P.O. Box 89, Sidi Bel Abbes 22000, Algeria
email: abdelli_mama@yahoo.fr
  Amira Rachah
Laboratoire de Mathématiques pour l'Industrie et la Physique
Institut de Mathématiques de Toulouse
Université Paul Sabatier
F-31062 Toulouse Cedex 9, France
email: amira.rachah@math.univ-toulouse.fr

Return to the EJDE web page