Electron. J. Differential Equations,
Vol. 2017 (2017), No. 52, pp. 1-14.
Ground state solutions for Choquard type equations with a
singular potential
Tao Wang
Abstract:
This article concerns the Choquard type equation

where
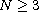 ,
,
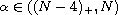 ,
,
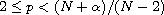 and V(x) is a possibly singular potential and may be unbounded below.
Applying a variant of the Lions' concentration-compactness principle,
we prove the existence of ground state solution of the above equations.
and V(x) is a possibly singular potential and may be unbounded below.
Applying a variant of the Lions' concentration-compactness principle,
we prove the existence of ground state solution of the above equations.
Submitted June 6, 2016. Published February 21, 2017.
Math Subject Classifications: 35A15, 35A20, 35J20.
Key Words: Choquard equation; singular potential; ground state solution;
Lions' concentration-compactness principle.
Show me the PDF file (273 KB),
TEX file for this article.
 |
Tao Wang
College of Mathematics and Computing Science
Hunan University of Science and Technology
Xiangtan, Hunan 411201, China
email: wt_61003@163.com
|
|---|
Return to the EJDE web page

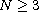 ,
,
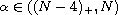 ,
,
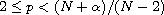 and V(x) is a possibly singular potential and may be unbounded below.
Applying a variant of the Lions' concentration-compactness principle,
we prove the existence of ground state solution of the above equations.
and V(x) is a possibly singular potential and may be unbounded below.
Applying a variant of the Lions' concentration-compactness principle,
we prove the existence of ground state solution of the above equations.
