In this article we study the p-biharmonic equation
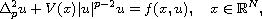
where
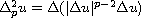 is the p-biharmonic
operator. When V(x) and f(x,u) satisfy some conditions, we prove that
the above equations have Nehari-type ground state solutions.
is the p-biharmonic
operator. When V(x) and f(x,u) satisfy some conditions, we prove that
the above equations have Nehari-type ground state solutions.
Xiaonan Liu, Haibo Chen, Belal Almuaalemi
Abstract:
In this article we study the p-biharmonic equation
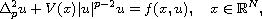
where
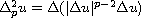 is the p-biharmonic
operator. When V(x) and f(x,u) satisfy some conditions, we prove that
the above equations have Nehari-type ground state solutions.
is the p-biharmonic
operator. When V(x) and f(x,u) satisfy some conditions, we prove that
the above equations have Nehari-type ground state solutions.
Submitted November 10, 2016. Published February 14, 2017.
Math Subject Classifications: 35B38, 35G99.
Key Words: p-biharmonic equations; Nehari manifold; ground state solution.
Show me the PDF file (232 KB), TEX file for this article.
 |
Xiaonan Liu School of Mathematics and Statistics Central South University Changsha, 410083 Hunan, China email: liuxiaonan20131110@163.com |
|---|---|
 |
Haibo Chen School of Mathematics and Statistics Central South University Changsha, 410083 Hunan, China email: math_chb@csu.edu.cn |
 |
Belal Almuaalemi School of Mathematics and Statistics Central South University Changsha, 410083 Hunan, China email: Belal_cn1980@hotmail.com |
Return to the EJDE web page