Electron. J. Differential Equations,
Vol. 2017 (2017), No. 40, pp. 1-10.
Periodic oscillations of the relativistic pendulum with friction
Qihuai Liu, Lukai Huang, Guirong Jiang
Abstract:
We consider the existence and multiplicity of periodic oscillations for
the forced pendulum model with relativistic effects by using the
Poincare-Miranda theorem. Some detailed information about the bound
for the period of forcing term is obtained. To support our analytical work,
we also consider a forced pendulum oscillator with the special force
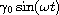 including a sufficiently small parameter.
The result shows us that for all
including a sufficiently small parameter.
The result shows us that for all
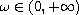 ,
there exists a
,
there exists a
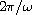 periodic solution under our settings.
periodic solution under our settings.
Submitted April 6, 2016. Published February 6, 2017.
Math Subject Classifications: 34B15.
Key Words: Relativistic pendulum; Poincare-Miranda theorem; averaging;
periodic solutions.
Show me the PDF file (237 KB),
TEX file for this article.
 |
Qihuai Liu
School of Mathematics and Computing Sciences
Guilin University of Electronic Technology
Guilin 541002, China
email: qhuailiu@gmail.com
|
|---|
 |
Lukai Huang
School of Mathematics and Computing Sciences
Guilin University of Electronic Technology
Guilin 541002, China
email: 756060523@qq.com
|
|---|
 |
Guirong Jiang
School of Mathematics and Computing Sciences
Guilin University of Electronic Technology
Guilin 541002, China
email: grjiang9@163.com
|
|---|
Return to the EJDE web page
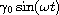 including a sufficiently small parameter.
The result shows us that for all
including a sufficiently small parameter.
The result shows us that for all
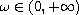 ,
there exists a
,
there exists a
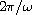 periodic solution under our settings.
periodic solution under our settings.


