Electron. J. Differential Equations,
Vol. 2017 (2017), No. 31, pp. 1-20.
A q-analogue of Kummer's equation
Lukun Jia, Jinfa Cheng, Zhaosheng Feng
Abstract:
In this article we define a q-analogue of Kummer's equation.
It has two singular points. Near the singular point at zero,
using the Frobenius method, we obtain two linearly independent series
solutions in any one of three cases according to the difference of roots
of the characteristic equation. Near the singular point at infinity,
given that the only formal series solution is divergent, we find two
integral solutions which are convergent under some condition. Finally,
using the q-analogue of Kummer's equation, we deduce six contiguous
relations about the q-hypergeometric series
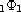 .
.
Submitted May 9, 2016. Published January 29, 2017.
Math Subject Classifications: 39A13, 39A05, 33D15.
Key Words: q-analogue, Kummer's equation; Frobenius method;
contiguous relations.
Show me the PDF file (269 KB),
TEX file for this article.
 |
Lukun Jia
School of Mathematical Science
Xiamen University
Xiamen, Fujian 361005, China
email: jialukun2005@163.com
|
|---|
 |
Jinfa Cheng
School of Mathematical Science
Xiamen University
Xiamen, Fujian 361005, China
email: jfcheng@xmu.edu.cn
|
|---|
 |
Zhaosheng Feng
School of Mathematical and Statistical Sciences
University of Texas-Rio Grande Valley
Edinburg, Texas 78539, USA
email: zhaosheng.feng@utrgv.edu
|
|---|
Return to the EJDE web page
 .
.


