Electron. J. Differential Equations,
Vol. 2017 (2017), No. 293, pp. 1-24.
Generalized uniformly continuous solution operators and inhomogeneous
fractional evolution equations with variable coefficients
Milos Japundzic, Danijela Rajter-Ciric
Abstract:
We consider Cauchy problem for inhomogeneous fractional evolution
equations with Caputo fractional derivatives of order
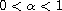 and variable coefficients depending on
and variable coefficients depending on
 .
In order to solve this
problem we introduce generalized uniformly continuous solution operators
and use them to obtain the unique solution on a certain Colombeau space.
In our solving procedure, instead of the original problem we solve a
certain approximate problem, but therefore we also prove that the
solutions of these two problems are associated. At the end, we illustrate
the applications of the developed theory by giving some appropriate examples.
.
In order to solve this
problem we introduce generalized uniformly continuous solution operators
and use them to obtain the unique solution on a certain Colombeau space.
In our solving procedure, instead of the original problem we solve a
certain approximate problem, but therefore we also prove that the
solutions of these two problems are associated. At the end, we illustrate
the applications of the developed theory by giving some appropriate examples.
Submitted October 21, 2016. Published November 27, 2017.
Math Subject Classifications: 35R11, 46F30, 26A33.
Key Words: Fractional evolution equation; fractional Duhamel principle;
generalized Colombeau solution operator; fractional derivative;
Mittag-Leffler type function.
Show me the PDF file (319 KB),
TEX file for this article.
 |
Milos Japundzic
Novi Sad Business School
Higher Education Institution for Applied Studies
Vladimira Perica-Valtera 4
21000 Novi Sad, Serbia
email: milos.japundzic@gmail.com
|
|---|
| |
Danijela Rajter-Ciric
Department of Mathematics and Informatics
Faculty of Science, University of Novi Sad
Trg Dositeja Obradovica 4
21000 Novi Sad, Serbia
email: rajter@dmi.uns.ac.rs
|
|---|
Return to the EJDE web page
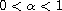 and variable coefficients depending on
and variable coefficients depending on
 .
In order to solve this
problem we introduce generalized uniformly continuous solution operators
and use them to obtain the unique solution on a certain Colombeau space.
In our solving procedure, instead of the original problem we solve a
certain approximate problem, but therefore we also prove that the
solutions of these two problems are associated. At the end, we illustrate
the applications of the developed theory by giving some appropriate examples.
.
In order to solve this
problem we introduce generalized uniformly continuous solution operators
and use them to obtain the unique solution on a certain Colombeau space.
In our solving procedure, instead of the original problem we solve a
certain approximate problem, but therefore we also prove that the
solutions of these two problems are associated. At the end, we illustrate
the applications of the developed theory by giving some appropriate examples.
