Electron. J. Differential Equations,
Vol. 2017 (2017), No. 29, pp. 1-19.
A characterisation of infinity-harmonic and p-harmonic maps via affine
variations in L-infinity
Nikos Katzourakis
Abstract:
Let
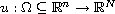 be a smooth map and
be a smooth map and
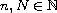 .
The
.
The
 -Laplacian
is the PDE system
-Laplacian
is the PDE system
![$$
\Delta_\infty u :=\Big(Du \otimes Du + |Du|^2[Du]^\bot \otimes I\Big) :D^2u = 0,
$$](gifs/ad.gif)
where
![$[Du]^\bot := \hbox{Proj}_{R(Du)^\bot}$](gifs/ae.gif) .
This system constitutes the fundamental equation of vectorial calculus
of variations in
.
This system constitutes the fundamental equation of vectorial calculus
of variations in
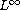 ,
associated with the model functional
,
associated with the model functional
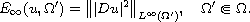
We show that generalised solutions to the system can be characterised in
terms of the functional via a set of designated affine variations.
For the scalar case N=1, we utilize the theory of viscosity solutions
by Crandall-Ishii-Lions. For the vectorial case
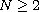 ,
we utilize
the recently proposed by the author theory of
,
we utilize
the recently proposed by the author theory of
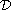 -solutions.
Moreover, we extend the result described above to the p-Laplacian,
-solutions.
Moreover, we extend the result described above to the p-Laplacian,
 .
.
Submitted August 10, 2016. Published January 26, 2017.
Math Subject Classifications: 35D99, 35D40, 35J47, 35J47, 35J92, 35J70, 35J99.
Key Words: Infinity-Laplacian; p-Laplacian; generalised solutions;
viscosity solutions; calculus of variations in L-infinity;
Young measures; fully nonlinear systems.
Show me the PDF file (338 KB),
TEX file for this article.
 |
Nikos Katzourakis
Department of Mathematics and Statistics
University of Reading, Whiteknights, PO Box 220
Reading RG6 6AX, Berkshire, UK
email: n.katzourakis@reading.ac.uk
|
|---|
Return to the EJDE web page
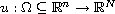 be a smooth map and
be a smooth map and
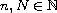 .
The
.
The
 -Laplacian
is the PDE system
-Laplacian
is the PDE system
![$$
\Delta_\infty u :=\Big(Du \otimes Du + |Du|^2[Du]^\bot \otimes I\Big) :D^2u = 0,
$$](gifs/ad.gif)
![$[Du]^\bot := \hbox{Proj}_{R(Du)^\bot}$](gifs/ae.gif) .
This system constitutes the fundamental equation of vectorial calculus
of variations in
.
This system constitutes the fundamental equation of vectorial calculus
of variations in
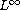 ,
associated with the model functional
,
associated with the model functional
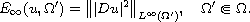
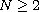 ,
we utilize
the recently proposed by the author theory of
,
we utilize
the recently proposed by the author theory of
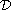 -solutions.
Moreover, we extend the result described above to the p-Laplacian,
-solutions.
Moreover, we extend the result described above to the p-Laplacian,
 .
.
