Electron. J. Differential Equations,
Vol. 2017 (2017), No. 282, pp. 1-13.
Least energy sign-changing solutions for the nonlinear
Schrodinger-Poisson system
Chao Ji, Fei Fang, Binlin Zhang
Abstract:
This article concerns the existence of the least energy sign-changing
solutions for the Schrodinger-Poisson system
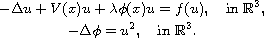
Because the so-called nonlocal term
 is involved in the
system, the variational functional of the above system has totally different
properties from the case of
is involved in the
system, the variational functional of the above system has totally different
properties from the case of
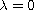 .
By constraint variational method
and quantitative deformation lemma, we prove that the above problem has one
least energy sign-changing solution. Moreover, for any
.
By constraint variational method
and quantitative deformation lemma, we prove that the above problem has one
least energy sign-changing solution. Moreover, for any
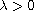 ,
we show that the energy of a sign-changing solution is strictly larger than
twice of the ground state energy. Finally, we consider
,
we show that the energy of a sign-changing solution is strictly larger than
twice of the ground state energy. Finally, we consider
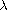 as a
parameter and study the convergence property of the least energy sign-changing
solutions as
as a
parameter and study the convergence property of the least energy sign-changing
solutions as
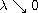 .
.
Submitted September 9, 2017. Published November 13, 2017.
Math Subject Classifications: 35J20, 35J60.
Key Words: Schrodinger-Poisson system; sign-changing solutions;
constraint variational method; quantitative deformation lemma.
Show me the PDF file (257 KB),
TEX file for this article.
 |
Chao Ji
Department of Mathematics
East China University of Science and Technology
Shanghai 200237, China
email: jichao@ecust.edu.cn
|
|---|
 |
Fei Fang
Department of Mathematics
Beijing Technology and Business University
Beijing 100048, China
email: fangfei68@163.com
|
|---|
 |
Binlin Zhang
Department of Mathematics
Heilongjiang Institute of Technology
Harbin 150050, China
email: zhangbinlin2012@163.com
|
|---|
Return to the EJDE web page
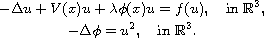
 is involved in the
system, the variational functional of the above system has totally different
properties from the case of
is involved in the
system, the variational functional of the above system has totally different
properties from the case of
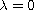 .
By constraint variational method
and quantitative deformation lemma, we prove that the above problem has one
least energy sign-changing solution. Moreover, for any
.
By constraint variational method
and quantitative deformation lemma, we prove that the above problem has one
least energy sign-changing solution. Moreover, for any
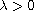 ,
we show that the energy of a sign-changing solution is strictly larger than
twice of the ground state energy. Finally, we consider
,
we show that the energy of a sign-changing solution is strictly larger than
twice of the ground state energy. Finally, we consider
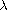 as a
parameter and study the convergence property of the least energy sign-changing
solutions as
as a
parameter and study the convergence property of the least energy sign-changing
solutions as
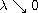 .
.


