Electron. J. Differential Equations,
Vol. 2017 (2017), No. 28, pp. 1-10.
Criteria and estimates for decaying oscillatory solutions for some
second-order quasilinear ODEs
Tadie
Abstract:
Oscillation criteria for the solutions of quasilinear second order ODE
are revisited. In our early works [6,7], we obtained basic
oscillation criteria for
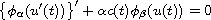
by estimating of the diameters of the nodal sets of the solutions.
The focus of this work is to estimate the decay of the oscillatory solutions.
Let u be a strongly oscillatory solution,
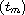 the increasing sequence
of zeros of u', and
the increasing sequence
of zeros of u', and
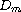 the nodal set of u that contains
the nodal set of u that contains
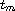 .
We estimate
.
We estimate
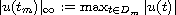 and the diameter of
and the diameter of
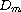 as
as
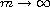 .
.
Submitted September 14, 2016. Published January 24, 2017.
Math Subject Classifications: 34C10, 34K15
Key Words: Oscillation criteria for ODE and Estimates of decaying solutions
Show me the PDF file (239 KB),
TEX file for this article.
 |
Tadie
Mathematics Institut
Universitetsparken 5
2100 Copenhagen, Denmark
email: tadietadie@yahoo.com
|
|---|
Return to the EJDE web page
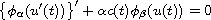
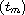 the increasing sequence
of zeros of u', and
the increasing sequence
of zeros of u', and
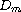 the nodal set of u that contains
the nodal set of u that contains
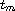 .
We estimate
.
We estimate
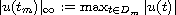 and the diameter of
and the diameter of
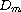 as
as
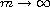 .
.
