Electron. J. Differential Equations,
Vol. 2017 (2017), No. 276, pp. 1-17.
Nonexistence of global solutions for fractional temporal
Schrodinger equations and systems
Ibtehal Azman, Mohamed Jleli, Mokhtar Kirane, Bessem Samet
Abstract:
We, first, consider the nonlinear Schrodinger equation
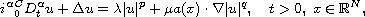
where
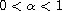 ,
,
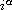 is the principal value of
is the principal value of
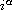 ,
,
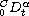 is the Caputo fractional derivative of
order
is the Caputo fractional derivative of
order
 ,
,
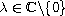 ,
,
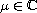 ,
,
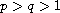 ,
,
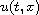 is a complex-valued function, and
is a complex-valued function, and
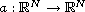 is a given vector function.
We provide sufficient conditions for the nonexistence of global weak solution
under suitable initial data. Next, we extend our study to the system of nonlinear
coupled equations
is a given vector function.
We provide sufficient conditions for the nonexistence of global weak solution
under suitable initial data. Next, we extend our study to the system of nonlinear
coupled equations
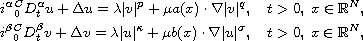
where
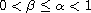 ,
,
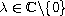 ,
,
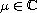 ,
,
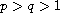 ,
,
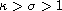 ,
and
,
and
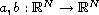 are two given vector functions.
Our approach is based on the test function method.
are two given vector functions.
Our approach is based on the test function method.
Submitted October 14, 2017. Published November 8, 2017.
Math Subject Classifications: 4735, 26A33.
Key Words: Fractional temporal Schrodinger equation;
nonexistence; global weak solution.
Show me the PDF file (286 KB),
TEX file for this article.
| |
Ibtehal Azman
Department of Mathematics
King Saud University,
P.O. Box 2455
Riyadh, 11451, Saudi Arabia
email: ibtehalazman@yahoo.com
|
|---|
 |
Mohamed Jleli
Department of Mathematics
King Saud University,
P.O. Box 2455,
Riyadh, 11451, Saudi Arabia
email: jleli@ksu.edu.sa
|
|---|
 |
Mokhtar Kirane
LaSIE, Faculté des Sciences
Pole Sciences et Technologies, Université de La Rochelle
Avenue M. Crepeau, 17042 La Rochelle Cedex, France
email: mkirane@univ-lr.fr
|
|---|
 |
Bessem Samet
Department of Mathematics
King Saud University,
P.O. Box 2455,
Riyadh, 11451, Saudi Arabia
email: bsamet@ksu.edu.sa
|
|---|
Return to the EJDE web page
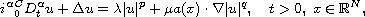
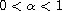 ,
,
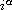 is the principal value of
is the principal value of
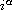 ,
,
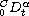 is the Caputo fractional derivative of
order
is the Caputo fractional derivative of
order
 ,
,
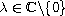 ,
,
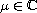 ,
,
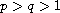 ,
,
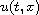 is a complex-valued function, and
is a complex-valued function, and
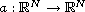 is a given vector function.
We provide sufficient conditions for the nonexistence of global weak solution
under suitable initial data. Next, we extend our study to the system of nonlinear
coupled equations
is a given vector function.
We provide sufficient conditions for the nonexistence of global weak solution
under suitable initial data. Next, we extend our study to the system of nonlinear
coupled equations
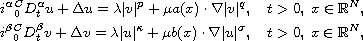
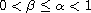 ,
,
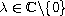 ,
,
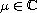 ,
,
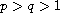 ,
,
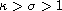 ,
and
,
and
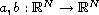 are two given vector functions.
Our approach is based on the test function method.
are two given vector functions.
Our approach is based on the test function method.


