This article concerns the nonlocal problem

where a, b are positive constants,
 is a non-negative parameter,
is a non-negative parameter,
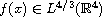 is a non-negative function.
By using the variational method, the existence of multiple positive solutions
are obtained.
is a non-negative function.
By using the variational method, the existence of multiple positive solutions
are obtained.
Yue Wang, Hong-Min Suo, Chun-Yu Lei
Abstract:
This article concerns the nonlocal problem

where a, b are positive constants,
 is a non-negative parameter,
is a non-negative parameter,
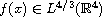 is a non-negative function.
By using the variational method, the existence of multiple positive solutions
are obtained.
is a non-negative function.
By using the variational method, the existence of multiple positive solutions
are obtained.
Submitted August 15, 2017. Published November 5, 2017.
Math Subject Classifications: 35A15, 35B09, 35B33.
Key Words: Multiple positive solutions; nonlocal problem; critical exponent.
Show me the PDF file (252 KB), TEX file for this article.
 |
Yue Wang School of Data Science and Information Engineering Guizhou Minzu University Guiyang 550025, China email: wyeztf@gmail.com |
|---|---|
 |
Hong-Min Suo School of Data Science and Information Engineering Guizhou Minzu University Guiyang 550025, China email: 11394861@qq.com |
 |
Chun-Yu Lei School of Data Science and Information Engineering Guizhou Minzu University Guiyang 550025, China email: leichygzu@sina.cn |
Return to the EJDE web page