Electron. J. Differential Equations,
Vol. 2017 (2017), No. 268, pp. 1-18.
Multiple nodal solutions of nonlinear Choquard equations
Zhihua Huang, Jianfu Yang, Weilin Yu
Abstract:
In this article, we consider the existence of multiple nodal
solutions of the nonlinear Choquard equation

where
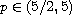 .
We show that for any positive integer k, the above
problem has at least one radially symmetrical solution changing sign
exactly k-times.
.
We show that for any positive integer k, the above
problem has at least one radially symmetrical solution changing sign
exactly k-times.
Submitted July 15, 2017. Published October 27, 2017.
Math Subject Classifications: 35J61, 35B33, 35B38, 35B65.
Key Words: Nonlinear Choquard equations; nodal solutions; nonlocal term.
Show me the PDF file (292 KB),
TEX file for this article.
| |
Zhihua Huang
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: zhhuang2016@126.com
|
|---|
 |
Jianfu Yang
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jfyang_2000@yahoo.com
|
|---|
| |
Weilin Yu
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: williamyu2065@163.com
|
|---|
Return to the EJDE web page

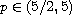 .
We show that for any positive integer k, the above
problem has at least one radially symmetrical solution changing sign
exactly k-times.
.
We show that for any positive integer k, the above
problem has at least one radially symmetrical solution changing sign
exactly k-times.
