Electron. J. Differential Equations,
Vol. 2017 (2017), No. 266, pp. 1-29.
Linearization of hyperbolic resonant fixed points of diffeomorphisms
with related Gevrey estimates in the planar case
Patrick Bonckaert, Vincent Naudot
Abstract:
We show that any germ of smooth hyperbolic diffeomophism at a fixed point
is conjugate to its linear part, using a transformation with a Mourtada type
functions, which (roughly) means that it may contain terms like
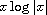 .
Such a conjugacy admits a Mourtada type expansion. In the planar case, when
the fixed point is a p:-q resonant saddle, and if we assume that the
diffeomorphism is of Gevrey class, we give an upper bound on the Gevrey
estimates for this expansion.
.
Such a conjugacy admits a Mourtada type expansion. In the planar case, when
the fixed point is a p:-q resonant saddle, and if we assume that the
diffeomorphism is of Gevrey class, we give an upper bound on the Gevrey
estimates for this expansion.
Submitted May 5, 2017. Published October 24, 2017.
Math Subject Classifications: 37C05, 37C27, 37G05.
Key Words: Poincare Dulac normal form; conjugacy; normal form;
Mourtada type function; tag monomial Gevrey asymptotic.
Show me the PDF file (353 KB),
TEX file for this article.
| |
Patrick Bonckaert
Hasselt University
Martelarenlaan 42
B-3500 Diepenbeek, Belgium
email: patrick.bonckaert@uhasselt.be
|
|---|
 |
Vincent Naudot
Dept of Mathematics
Florida Atlantic University
777 Glades Road
Boca Raton, FL 33433, USA
email: vnaudot@fau.edu
|
|---|
Return to the EJDE web page
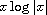 .
Such a conjugacy admits a Mourtada type expansion. In the planar case, when
the fixed point is a p:-q resonant saddle, and if we assume that the
diffeomorphism is of Gevrey class, we give an upper bound on the Gevrey
estimates for this expansion.
.
Such a conjugacy admits a Mourtada type expansion. In the planar case, when
the fixed point is a p:-q resonant saddle, and if we assume that the
diffeomorphism is of Gevrey class, we give an upper bound on the Gevrey
estimates for this expansion.
