Electron. J. Differential Equations,
Vol. 2017 (2017), No. 262, pp. 1-12.
Existence of solutions to a boundary-value problem for an infinite
system of differential equations
Jozef Banas, Mohammad Mursaleen, Syed M. H. Rizvi
Abstract:
Using techniques associated with measures of noncompactness we prove
an existence of solutions for a boundary-value problem for an infinite
system of ordinary differential equations of second order.
Our approach depends on transforming of the original boundary-value problem
into an infinite system of integral equations of Fredholm type.
The settings for this article are in the classical Banach sequence
space
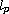 with
with
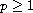 .
.
Submitted August 3, 2017. Published October 17, 2017.
Math Subject Classifications: 34G20, 47H08.
Key Words: Measure of noncompactness; equicontinuous family;
boundary value problem; infinite system of differential equations;
Fredholm integral equation.
Show me the PDF file (218 KB),
TEX file for this article.
 |
Jozef Banas
Department of Nonlinear Analysis
Rzeszow University of Technology
al. Powstancow Warszawy 8, 35-959 Rzeszow, Poland
email: jbanas@prz.edu.pl
|
|---|
 |
Mohammad Mursaleen
Department of Mathematics
Aligarh Muslim University
Aligarh 202002, India
email: mursaleenm@gmail.com
|
|---|

| Syed M. H. Rizvi
Department of Mathematics
Aligarh Muslim University
Aligarh 202002, India
email: syedrizvi022@gmail.com
|
|---|
Return to the EJDE web page
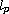 with
with
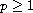 .
.


