Electron. J. Differential Equations,
Vol. 2017 (2017), No. 249, pp. 1-13.
Pairs of positive solutions for resonant singular equations with the p-Laplacian
Nikolaos S. Papageorgiou, Vicentiu D. Radulescu, Dusan D. Repovs
Abstract:
We consider a nonlinear elliptic equation driven by the Dirichlet
p-Laplacian with a singular term and a (p-1)-linear perturbation
which is resonant at
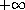 with respect to the principal eigenvalue.
Using variational tools, together with suitable truncation and comparison
techniques, we show the existence of at least two positive smooth solutions.
with respect to the principal eigenvalue.
Using variational tools, together with suitable truncation and comparison
techniques, we show the existence of at least two positive smooth solutions.
Submitted June 29, 2017. Published October 6, 2017.
Math Subject Classifications: 35J20, 35J25, 35J67.
Key Words: Singular reaction; resonance; regularity; positive solutions;
maximum principle; mountain pass theorem.
Show me the PDF file (259 KB),
TEX file for this article.
| |
Nikolaos S. Papageorgiou
National Technical University
Department of Mathematics
Zografou Campus, Athens 15780, Greece
email: npapg@math.ntua.gr
|
|---|
 |
Vicentiu D. Radulescu
Department of Mathematics, Faculty of Sciences
King Abdulaziz University, P.O. Box 80203
Jeddah 21589, Saudi Arabia
email: radulescu@inf.ucv.ro
|
|---|
 |
Dusan D. Repovs
Faculty of Education and Faculty of Mathematics and Physics
University of Ljubljana
SI-1000 Ljubljana, Slovenia
email: dusan.repovs@guest.arnes.si
|
|---|
Return to the EJDE web page
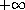 with respect to the principal eigenvalue.
Using variational tools, together with suitable truncation and comparison
techniques, we show the existence of at least two positive smooth solutions.
with respect to the principal eigenvalue.
Using variational tools, together with suitable truncation and comparison
techniques, we show the existence of at least two positive smooth solutions.

