Electron. J. Differential Equations,
Vol. 2017 (2017), No. 247, pp. 1-17.
Antiperiodic solutions to van der Pol equations with state-dependent impulses
Irena Rachunkova, Jan Tomecek
Abstract:
In this article we give sufficient conditions for the existence of an
antiperiodic solution to the van der Pol equation
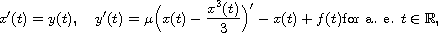
subject to a finite number of state-dependent impulses

Our approach is based on the reformulation of the problem as a distributional
differential equation and on the Schauder fixed point theorem.
The functionals
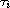 and
and
 need not be Lipschitz continuous
nor bounded. As a direct consequence, we obtain an existence result for
problem with fixed-time impulses.
need not be Lipschitz continuous
nor bounded. As a direct consequence, we obtain an existence result for
problem with fixed-time impulses.
Submitted June 2, 2017. Published October 6, 2017.
Math Subject Classifications: 34A37, 34B37.
Key Words: van der Pol equation; state-dependent impulses; existence;
distributional equation; periodic distributions; antiperiodic solution.
Show me the PDF file (321 KB),
TEX file for this article.
 |
Irena Rachunkova
Department of Mathematical Analysis
and Applications of Mathematics
Faculty of Science, Palacky University
17. Listopadu 12, 771 46 Olomouc, Czechia
email: irena.rachunkova@upol.cz
|
|---|
 |
Jan Tomecek
Department of Mathematical Analysis
and Applications of Mathematics
Faculty of Science, Palacky University
17. Listopadu 12, 771 46 Olomouc, Czechia
email: jan.tomecek@upol.cz
|
|---|
Return to the EJDE web page
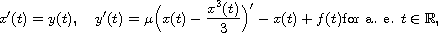

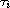 and
and
 need not be Lipschitz continuous
nor bounded. As a direct consequence, we obtain an existence result for
problem with fixed-time impulses.
need not be Lipschitz continuous
nor bounded. As a direct consequence, we obtain an existence result for
problem with fixed-time impulses.

