Electron. J. Differential Equations,
Vol. 2017 (2017), No. 240, pp. 1-16.
Positive solutions for superlinear Riemann-Liouville fractional
boundary-value problems
Imed Bachar, Habib Maagli, Vicentiu D. Radulescu
Abstract:
Using a perturbation argument, we establish the existence and uniqueness of a
positive continuous solution for the following superlinear Riemann-Liouville
fractional boundary-value problem

where
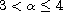 and
and
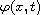 satisfies a suitable
integrability condition.
satisfies a suitable
integrability condition.
Submitted August 18, 2017. Published October 4, 2017.
Math Subject Classifications: 34A08, 34B15, 34B18, 34B27.
Key Words: Fractional differential equation; positive solution;
Green's function; perturbation; Schauder fixed point theorem.
Show me the PDF file (275 KB),
TEX file for this article.
 |
Imed Bachar
King Saud University
Department of Mathematics, College of Science
P.O. Box 2455, Riyadh 11451, Saudi Arabia
email: abachar@ksu.edu.sa
|
|---|
 |
Habib Mâagli
Department of Mathematics
College of Sciences and Arts
King Abdulaziz University
Rabigh Campus P.O. Box 344
Rabigh 21911, Saudi Arabia
email: abobaker@kau.edu.sa, habib.maagli@fst.rnu.tn
|
|---|
 |
Vicentiu D. Radulescu
Department of Mathematics
Faculty of Sciences
King Abdulaziz University
P.O. Box 80203, Jeddah 21589, Saudi Arabia
email: vicentiu.radulescu@math.cnrs.fr
|
|---|
Return to the EJDE web page

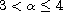 and
and
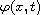 satisfies a suitable
integrability condition.
satisfies a suitable
integrability condition.


