Electron. J. Differential Equations,
Vol. 2017 (2017), No. 226, pp. 1-11.
Uniqueness theorems for Sturm-Liouville operators with interior
twin-dense nodal set
Yu Ping Wang
Abstract:
We study Inverse problems for the Sturm-Liouville operator with Robin boundary
conditions. We establish two uniqueness theorems from the twin-dense nodal
subset
![$W_{S}([\frac{1-\varepsilon}{2},\frac{1}{2}])$](gifs/aa.gif) ,
,
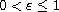 ,
together with parts of either one spectrum, or the
minimal nodal subset
,
together with parts of either one spectrum, or the
minimal nodal subset
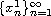 on the interval [0,1/2].
In particular, if one spectrum is given a priori, then the potential q on
the whole interval [0,1] can be uniquely determined by
on the interval [0,1/2].
In particular, if one spectrum is given a priori, then the potential q on
the whole interval [0,1] can be uniquely determined by
![$W_{S}([\frac{1-\varepsilon}{2},\frac{1}{2}])$](gifs/ad.gif) for any S and arbitrarily small
for any S and arbitrarily small
 .
.
Submitted September 19, 2016. Published September 20, 2017.
Math Subject Classifications: 34A55, 34B24, 47E05.
Key Words: Uniqueness theorem; inverse nodal problem; potential;
Sturm-Liouville operator; the interior twin-dense nodal subset.
Show me the PDF file (266 KB),
TEX file for this article.
 |
Yu Ping Wang
Department of Applied Mathematics
Nanjing Forestry University
Nanjing, Jiangsu 210037, China
email: ypwang@njfu.com.cn
|
|---|
Return to the EJDE web page
![$W_{S}([\frac{1-\varepsilon}{2},\frac{1}{2}])$](gifs/aa.gif) ,
,
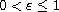 ,
together with parts of either one spectrum, or the
minimal nodal subset
,
together with parts of either one spectrum, or the
minimal nodal subset
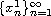 on the interval [0,1/2].
In particular, if one spectrum is given a priori, then the potential q on
the whole interval [0,1] can be uniquely determined by
on the interval [0,1/2].
In particular, if one spectrum is given a priori, then the potential q on
the whole interval [0,1] can be uniquely determined by
![$W_{S}([\frac{1-\varepsilon}{2},\frac{1}{2}])$](gifs/ad.gif) for any S and arbitrarily small
for any S and arbitrarily small
 .
.
