Electron. J. Differential Equations,
Vol. 2017 (2017), No. 204, pp. 1-25.
Positive solutions for nonlinear Robin problems
Diego Averna, Nikolaos S. Papageorgiou, Elisabetta Tornatore
Abstract:
We consider a parametric Robin problem driven by the p-Laplacian with
an indefinite potential and with a superlinear reaction term which does
not satisfy the Ambrosetti-Rabinowitz condition.
We look for positive solutions. We prove a bifurcation-type theorem
describing the nonexistence, existence and multiplicity of positive
solutions as the parameter varies. We also show the existence of a minimal
positive solution
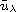 and establish the monotonicity and
continuity of the map
and establish the monotonicity and
continuity of the map
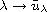 .
.
Submitted June 7, 2017. Published September 6, 2017.
Math Subject Classifications: 35J25, 35J80
Key Words: Robin boundary condition; superlinear reaction;
truncation and comparison techniques; bifurcation-type result;
minimax positive solution.
Show me the PDF file (350 KB),
TEX file for this article.
 |
Diego Averna
Dipartimento di Matematica e Informatica
Università degli studi di Palermo
Via Archirafi, 90123 - Palermo, Italy
email: diego.averna@unipa.it
|
|---|
| |
Nikolaos S. Papageorgiou
Department of Mathematics
National Technical University
Zografou Campus, Athens 15780, Greece
email: npapg@math.ntua.gr
|
|---|
 |
Elisabetta Tornatore
Dipartimento di Matematica e Informatica
Università degli studi di Palermo
Via Archirafi, 90123 Palermo, Italy
email: elisa.tornatore@unipa.it
|
|---|
Return to the EJDE web page
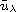 and establish the monotonicity and
continuity of the map
and establish the monotonicity and
continuity of the map
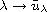 .
.

