Electron. J. Differential Equations,
Vol. 2017 (2017), No. 19, pp. 1-15.
Semiclassical solutions of perturbed biharmonic equations with critical
nonlinearity
Yubo He, Xianhua Tang, Wen Zhang
Abstract:
We consider the perturbed biharmonic equations
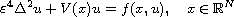
and
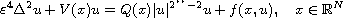
where
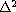 is the biharmonic operator,
is the biharmonic operator,
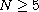 ,
,
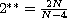 is the Sobolev critical exponent,
Q(x) is a bounded positive function. Under some mild conditions on
V and f, we show that the above equations have at least one
nontrivial solution provided that
is the Sobolev critical exponent,
Q(x) is a bounded positive function. Under some mild conditions on
V and f, we show that the above equations have at least one
nontrivial solution provided that
 ,
where the bound
,
where the bound
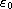 is formulated in terms of N, V, Q and f.
is formulated in terms of N, V, Q and f.
Submitted November 15, 2016. Published January 16, 2017.
Math Subject Classifications: 35J35, 35J60, 58E05, 58E50.
Key Words: Perturbed biharmonic equation; semiclassical solution;
critical nonlinearity.
Show me the PDF file (279 KB),
TEX file for this article.
 |
Yubo He
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: hybmath@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: tangxh@mail.csu.edu.cn
|
|---|
 |
Wen Zhang
School of Mathematics and Statistics
Hunan University of Commerce
Changsha, 410205 Hunan, China
email: zwmath2011@163.com
|
|---|
Return to the EJDE web page
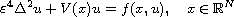
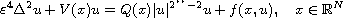
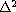 is the biharmonic operator,
is the biharmonic operator,
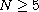 ,
,
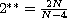 is the Sobolev critical exponent,
Q(x) is a bounded positive function. Under some mild conditions on
V and f, we show that the above equations have at least one
nontrivial solution provided that
is the Sobolev critical exponent,
Q(x) is a bounded positive function. Under some mild conditions on
V and f, we show that the above equations have at least one
nontrivial solution provided that
 ,
where the bound
,
where the bound
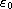 is formulated in terms of N, V, Q and f.
is formulated in terms of N, V, Q and f.


