Electron. J. Differential Equations,
Vol. 2017 (2017), No. 187, pp. 1-18.
Second-order boundary estimate for the solution to infinity Laplace equations
Ling Mi
Abstract:
In this article, we establish a second-order estimate for the solutions
to the infinity Laplace equation
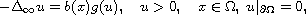
where
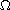 is a bounded domain in
is a bounded domain in
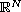 ,
,
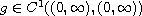 ,
,
 is decreasing on
is decreasing on
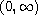 with
with
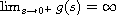 and g is normalized regularly varying at
zero with index
and g is normalized regularly varying at
zero with index
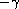 (
(
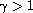 ),
),
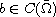 is
positive in
is
positive in
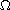 ,
may be vanishing on the boundary. Our analysis is
based on Karamata regular variation theory.
,
may be vanishing on the boundary. Our analysis is
based on Karamata regular variation theory.
Submitted December 18, 2016. Published July 24, 2017.
Math Subject Classifications: 35J55, 35J60, 35J65.
Key Words: Infinity Laplace equation; second order estimate;
Karamata regular variation theory; comparison functions.
Show me the PDF file (289 KB),
TEX file for this article.
 |
Ling Mi
College of Mathematics and Statistics
Linyi University
Linyi, Shang Dong 276005, China
email: mi-ling@163.com, miling@lyu.edu.cn
|
|---|
Return to the EJDE web page
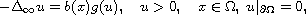
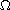 is a bounded domain in
is a bounded domain in
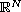 ,
,
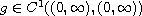 ,
,
 is decreasing on
is decreasing on
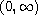 with
with
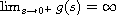 and g is normalized regularly varying at
zero with index
and g is normalized regularly varying at
zero with index
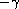 (
(
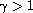 ),
),
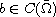 is
positive in
is
positive in
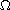 ,
may be vanishing on the boundary. Our analysis is
based on Karamata regular variation theory.
,
may be vanishing on the boundary. Our analysis is
based on Karamata regular variation theory.
