Electron. J. Differential Equations,
Vol. 2017 (2017), No. 184, pp. 1-12.
Existence of solutions for Kirchhoff type equations with
unbounded potential
Yueliang Duan, Yinggao Zhou
Abstract:
In this article, we study the Kirchhoff type equation
![$$
\Big(a+\lambda\int_{\mathbb{R}^3}|\nabla u|^2
+\lambda b\int_{\mathbb{R}^3}u^2\Big)[-\Delta u+b u]
=K(x)|u|^{p-1}u,\quad \text{in } \mathbb{R}^3,
$$](gifs/aa.gif)
where
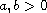 ,
,
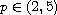 ,
,
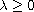 is a parameter, and
K may be an unbounded potential function. By using variational methods,
we prove the existence of nontrivial solutions for the above equation.
A cut-off functional and some estimates are used to obtain the bounded
Palais-Smale sequences.
is a parameter, and
K may be an unbounded potential function. By using variational methods,
we prove the existence of nontrivial solutions for the above equation.
A cut-off functional and some estimates are used to obtain the bounded
Palais-Smale sequences.
Submitted March 7, 2017. Published July 19, 2017.
Math Subject Classifications: 35A15, 35A20, 35J20.
Key Words: Cut-off functional; Kirchhoff type problem; unbounded potential;
variational method.
Show me the PDF file (248 KB),
TEX file for this article.
 |
Yueliang Duan
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: duanyl@csu.edu.cn
|
|---|
 |
Yinggao Zhou
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: ygzhou@mail.csu.edu.cn
|
|---|
Return to the EJDE web page
![$$
\Big(a+\lambda\int_{\mathbb{R}^3}|\nabla u|^2
+\lambda b\int_{\mathbb{R}^3}u^2\Big)[-\Delta u+b u]
=K(x)|u|^{p-1}u,\quad \text{in } \mathbb{R}^3,
$$](gifs/aa.gif)
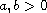 ,
,
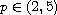 ,
,
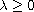 is a parameter, and
K may be an unbounded potential function. By using variational methods,
we prove the existence of nontrivial solutions for the above equation.
A cut-off functional and some estimates are used to obtain the bounded
Palais-Smale sequences.
is a parameter, and
K may be an unbounded potential function. By using variational methods,
we prove the existence of nontrivial solutions for the above equation.
A cut-off functional and some estimates are used to obtain the bounded
Palais-Smale sequences.

