Electron. J. Differential Equations,
Vol. 2017 (2017), No. 164, pp. 1-13.
Ground state solutions for Hamiltonian elliptic system
with sign-changing potential
Wen Zhang, Xiaoliang Xie, Heilong Mi
Abstract:
This article concerns the Hamiltonian elliptic system
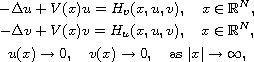
where
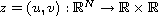 ,
,
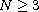 and the potential V(x) is allowed to be sign-changing. Under weak
superquadratic assumptions for the nonlinearities, by applying the variant
generalized weak linking theorem for strongly indefinite problem developed
by Schechter and Zou, we obtain the existence of nontrivial and ground state
solutions.
and the potential V(x) is allowed to be sign-changing. Under weak
superquadratic assumptions for the nonlinearities, by applying the variant
generalized weak linking theorem for strongly indefinite problem developed
by Schechter and Zou, we obtain the existence of nontrivial and ground state
solutions.
Submitted March 21, 2017. Published July 4, 2017.
Math Subject Classifications: 35J50, 35J55.
Key Words: Hamiltonian elliptic system; superquadratic; sign-changing potential;
generalized weak linking theorem.
Show me the PDF file (273 KB),
TEX file for this article.
 |
Wen Zhang
School of Mathematics and Statistics
Hunan University of Commerce
Changsha, 410205 Hunan, China
email: zwmath2011@163.com
|
|---|
 |
Xiaoliang Xie
School of Mathematics and Statistics and
Key Laboratory of Hunan Province for Mobile Business Intelligence
Hunan University of Commerce
Changsha, 410205 Hunan, China
email: xiexiaoliangmath@163.com
|
|---|
 |
Heilong Mi
School of Mathematics and Statistics
Hunan University of Commerce
Changsha, 410205 Hunan, China
email: 691473547@qq.com
|
|---|
Return to the EJDE web page
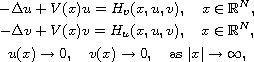
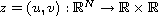 ,
,
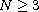 and the potential V(x) is allowed to be sign-changing. Under weak
superquadratic assumptions for the nonlinearities, by applying the variant
generalized weak linking theorem for strongly indefinite problem developed
by Schechter and Zou, we obtain the existence of nontrivial and ground state
solutions.
and the potential V(x) is allowed to be sign-changing. Under weak
superquadratic assumptions for the nonlinearities, by applying the variant
generalized weak linking theorem for strongly indefinite problem developed
by Schechter and Zou, we obtain the existence of nontrivial and ground state
solutions.


