In this article we study the traveling wave solutions of a monostable nonlocal reaction-diffusion system with delay arising from the spread of an epidemic by oral-faecal transmission. From [23], there exists a minimal wave speed
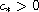 such that a
traveling wave solution exists if and only if the wave speed is above
such that a
traveling wave solution exists if and only if the wave speed is above
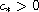 .
In this article, we first establish the exact asymptotic behavior of the
traveling waves at
.
In this article, we first establish the exact asymptotic behavior of the
traveling waves at
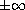 .
Then, we construct some annihilating-front
entire solutions which behave like a traveling wave front propagating from
the left side (or the right side) on the x-axis or two traveling wave fronts
propagating from both sides on the x-axis as
.
Then, we construct some annihilating-front
entire solutions which behave like a traveling wave front propagating from
the left side (or the right side) on the x-axis or two traveling wave fronts
propagating from both sides on the x-axis as
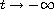 and converge
to the unique positive equilibrium as
and converge
to the unique positive equilibrium as
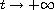 .
From the viewpoint of epidemiology, these results provide some new spread
ways of the epidemic.
.
From the viewpoint of epidemiology, these results provide some new spread
ways of the epidemic.
