Electron. J. Differential Equations,
Vol. 2017 (2017), No. 153, pp. 1-21.
Two-dimensional product-type systems of difference equations of
delay-type (2,2,1,2)
Stevo Stevic
Abstract:
We prove that the following class of systems of difference equations
is solvable in closed form:
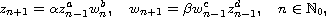
where
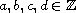 ,
,
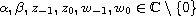 .
We present formulas for its solutions in all the cases. The most complex
formulas are presented in terms of the zeros of three different associated
polynomials to the systems corresponding to the cases a=0, c=0 and
.
We present formulas for its solutions in all the cases. The most complex
formulas are presented in terms of the zeros of three different associated
polynomials to the systems corresponding to the cases a=0, c=0 and
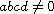 ,
respectively, which on the other hand depend on some of
parameters a, b, c, d.
,
respectively, which on the other hand depend on some of
parameters a, b, c, d.
Submitted April 21, 2017. Published June 27, 2017.
Math Subject Classifications: 39A20, 39A45.
Key Words: System of difference equations; product-type system;
solvable in closed form.
Show me the PDF file (360 KB),
TEX file for this article.
 |
Stevo Stevic
Mathematical Institute of the Serbian Academy of Sciences
Knez Mihailova 36/III
11000 Beograd, Serbia
email: sstevic@ptt.rs
|
|---|
Return to the EJDE web page
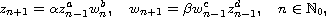
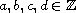 ,
,
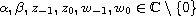 .
We present formulas for its solutions in all the cases. The most complex
formulas are presented in terms of the zeros of three different associated
polynomials to the systems corresponding to the cases a=0, c=0 and
.
We present formulas for its solutions in all the cases. The most complex
formulas are presented in terms of the zeros of three different associated
polynomials to the systems corresponding to the cases a=0, c=0 and
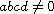 ,
respectively, which on the other hand depend on some of
parameters a, b, c, d.
,
respectively, which on the other hand depend on some of
parameters a, b, c, d.
