Electron. J. Differential Equations, Vol. 2017 (2017), No. 150, pp. 1-12.

An alternative approach to critical PDEs

Nikos Labropoulos

Abstract:
In this article, we use an alternative method to prove the existence of an infinite sequence of distinct non-radial nodal G-invariant solutions for critical nonlinear elliptic problems defined in the whole the Euclidean space. Our proof is via approximation of the problem on symmetric bounded domains. The base model problem of interest originating from Physics is stated below:
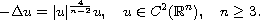
$$ -\Delta u = |u|^{\frac{4}{n-2}}u ,\quad u\in C^2(\mathbb{R}^n), \quad n\geq3. $$

Submitted March 8, 2017. Published June 23, 2017.
Math Subject Classifications: 35J60, 35B33, 35J20.
Key Words: Laplacian; non-radial solution; critical exponent.

Show me the PDF file (248 KB), TEX file for this article.

Nikos Labropoulos
Department of Mathematics
University of Patras
Patras 26110, Greece
email: nal@upatras.gr

Return to the EJDE web page